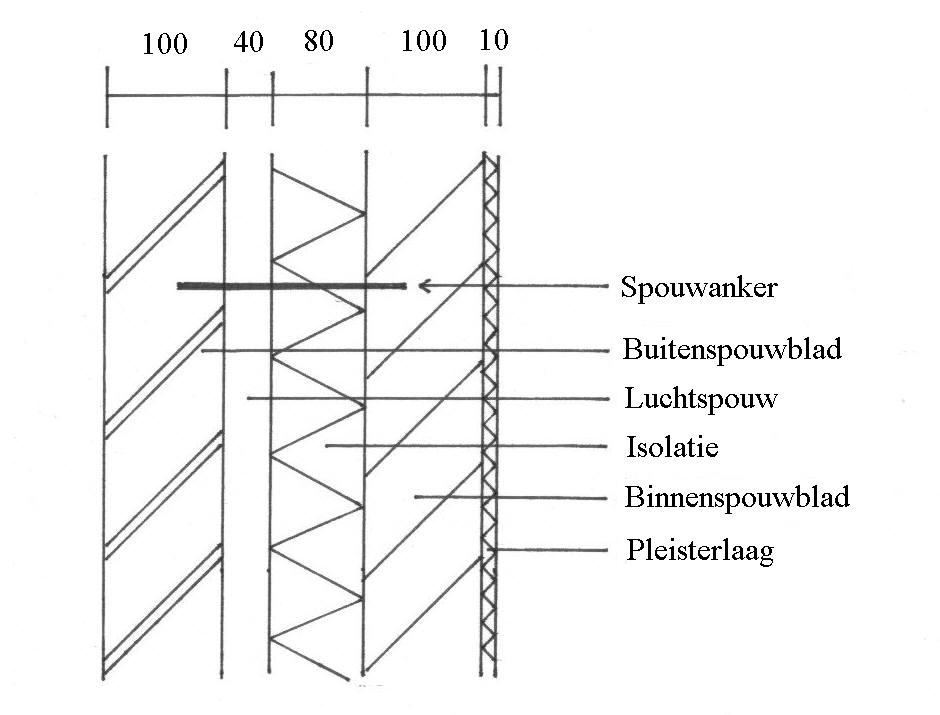
Figuur 1. Doorsnede van een spouwmuur.
De isolatie calculator.
Met de hier gepresenteerde "isolatie calculator" kun je de
warmteweerstand en U-waarde van een bouwkundige constructie berekenen, b.v. van
een dak of wand van een huis.
En vervolgens kun je daarmee uitrekenen hoeveel warmteverlies de constructie
per jaar geeft.
Hiermee is het ook mogelijk om van te voren uit te rekenen hoeveel energie je
gaat besparen door het aanbrengen van extra warmte-isolatie.
Onder de calculator staat een uitleg over het gebruik ervan, en over de
achterliggende formules.
Gebruik van de isolatie calculator
Het gebruik van de isolatie calculator zal ik uitleggen aan de hand van een
praktijk voorbeeld.
In dit voorbeeld gaan we met de calculator de warmtedoorgangscoŽfficient
(U-waarde) van een spouwmuur bepalen.
En vervolgens het energieverlies door deze spouwmuur.

Figuur 1. Doorsnede van een spouwmuur.
Een bouwkundige constructie bestaat uit ťťn of meerdere materiaallagen.
In de calculator gaan we nu van elke laag de λ
waarde en de laagdikte invullen.
Voor de spouwmuur uit figuur 1 zijn dat van buiten naar binnen de volgende 5 lagen:
Laag 1: een buitenspouwblad van baksteen (nat), 100 mm dik,
λ = 1,289 W/mK
Laag 2: een zwak geventileerde luchtspouw van 40 mm.
Laag 3: een laag PIR isolatiemateriaal van 80 mm dik,
λ = 0,028 W/mK
Laag 4: een binnenspouwblad van kalkzandsteen (droog), 100 mm dik,
λ = 1,126 W/mK
Laag 5: een pleisterlaag van cement (droog), 10 mm dik
λ = 0,93 W/mK
Selecteer in de calculator voor alle 5 de lagen, het materiaal waaruit ze
bestaan.
De λ waarde wordt dan vanzelf ingevuld.
Je kunt ook zelf een λ waarde invullen als een bepaald materiaal niet in de
lijst staat.
Ook kun je de λ waarde van een geselecteerd materiaal nog zelf wijzigen.
Voor een luchtspouw hoef je geen λ waarde in te vullen, de calculator rekent
deze later zelf uit.
Als een materiaal nat kan worden door
regenwater, selecteer dan dat materiaal in natte toestand.
In dit geval betreft dat alleen het bakstenen buitenspouwblad.
Tussen het binnenspouwblad en buitenspouwblad bevinden zich ook nog stalen spouwankers,
deze staan parallel aan de lagen 2 en 3.
Er zijn bijvoorbeeld 4 spouwankers per vierkante meter muur.
…ťn spouwanker heeft (bijvoorbeeld) een oppervlakte van 12,5 mm≤.
Dat is totaal dus 50 mm≤ spouwanker per m≤ muur, ofwel 0,005 % van de
oppervlakte.
In zowel laag 2 als 3 vullen we dus in:
Parallel materiaal: staal λ = 50 en percentage: 0,005 %.
Nu moeten we de soort constructie selecteren, in
dit geval moet dat zijn:
"Wanden en overige constructies grenzend aan buitenlucht"
Selecteer dan de rekenmethode, ik gebruik de methode NEN1068 met correctiefactor α = 0,05.
Klik nu op de knop "Bereken R en U waarden".
Dit geeft als antwoord:
Rc = 2,744 m≤K/W
Rtotaal = 2,914 m≤K/W
U = 0,343 W/m≤K
Vul nu de oppervlakte van de constructie in, ik
laat deze nu even op 1 m≤ staan.
Het aantal gewogen graaddagen laat ik op 2900 per jaar staan.
Klik nu op "bereken warmtestroom en energieverlies"
En het blijkt dat 1 m≤ van deze spouwmuur een energieverlies van zo'n 2,866 m≥ gas per
jaar geeft.
Nu kun je allerlei wijzigingen op de constructie
loslaten, b.v. een dikkere isolatielaag, of juist helemaal geen isolatie, en
zien wat dit met het energieverlies doet.
Ook kun je de spouwankers van roestvast staal kiezen, dit geeft minder
energieverlies dan stalen spouwankers.
Als je een bepaalde laag niet mee wilt nemen in
de berekening (omdat je minder dan 5 materiaallagen hebt), laat dan het veld met
de λ waarde leeg.
En selecteer dan ook geen luchtspouw, want in dat geval gaat de calculator zelf
een λ waarde berekenen en invullen.
Hopelijk geeft de isolatie calculator je wat
inzicht in de energieverliezen welke in een bouwconstructie optreden.
En is het een handig hulpmiddel voor degenen die met isolatiemaatregelen aan de
slag willen.
Hieronder volgt nog een uitleg over de in de calculator gebruikte grootheden en formules.
WarmtegeleidingscoŽfficiŽnt λ
De warmtegeleidingscoŽfficiŽnt ofwel de λ waarde (labda waarde) van een
materiaal geeft aan hoe goed een materiaal warmte geleidt.
Goede warmtegeleiders (zoals metalen) hebben een hoge λ waarde.
Warmte isolators hebben een lage λ waarde.
De eenheid voor de warmtegeleidingscoŽfficiŽnt λ is: W/mK
Op diverse websites,
kun je tabellen vinden met de
λ waarde van vele bouwmaterialen.
Let erop dat de λ waarde van een materiaal sterk kan variŽren, afhankelijk van
het soortelijk gewicht van het materiaal.
Hoe groter het soortelijk gewicht, hoe hoger de λ waarde.
Ook zijn vele materialen gevoelig voor vocht, de λ waarde van zo'n materiaal in
vochtige toestand is hoger dan in droge toestand.
De vochtige waarde is van toepassing als een materiaal door regen nat kan
worden, b.v. een buitenmuur, maar ook het isolatiemateriaal dat daarmee in
direct contact is.
Als er gesproken wordt over "λ rekenwaarde", bedoelt men de λ waarde van het
materiaal in natte toestand.
Warmteweerstand van een vlakke laag
De warmteweerstand (Rm) van vlakke homogene laag wordt berekend met:
Formule 1:
Rm=d/λ
eenheid: m≤K/W
Waarbij:
λ = de warmtegeleidingscoŽfficiŽnt in W/mK.
d = dikte van de laag in m (meter).
Warmteweerstand van een laag wanneer twee
materialen parallel staan.
Wanneer de laag bestaat uit twee verschillende materialen
welke parallel staan, moeten we de warmtegeleidingscoŽfficiŽnt λ eerst als volgt berekenen:
Formule 2:
λ = (λ1 . A1 + λ2.A2) / (A1+A2)
Waarbij:
λ1 = warmtegeleidingscoŽfficiŽnt van materiaal 1
λ2 = warmtegeleidingscoŽfficiŽnt van materiaal 2.
A1 = oppervlakte van materiaal 1 in m≤.
A2 = oppervlakte van materiaal 2 in m≤.
Vervolgens berekenen we de warmteweerstand van
de laag, alsof het een homogene laag is, dus weer met formule 1:
Rm=d/λ
eenheid: m≤K/W
Een voorbeeld van twee materialen parallel is;
een spouwmuur waar de metalen spouwankers parallel staan aan de (al dan niet
geÔsoleerde) spouw.
Overgangsweerstand Rsi en Rse
Wanneer een materiaallaag grenst aan lucht, hebben we te maken met een
thermische overgangsweerstand tussen materiaal en lucht.
Deze overgangsweerstand wordt veroorzaakt door een min of meer stilstaand laagje
lucht, direct grenzend aan het materiaal.
We kunnen hierbij twee verschillende overgangsweerstanden onderscheiden,
namelijk:
Rsi = Overgangsweerstand van materiaal naar
lucht aan de binnen- ( warmste-) zijde van de constructie.
en
Rse = Overgangsweerstand van materiaal naar lucht aan de buiten- ( koudste-) zijde van de
constructie.
De waarden van Rsi en Rse zijn afhankelijk van de aard van de bouwkundige constructie volgens onderstaande tabel:
|
Soort constructie |
Rsi (m≤K/W) |
Rse (m≤K/W) |
| Daken met hellingshoek met horizontaal t/m 75 į | 0,10 | 0,04 |
| Vloer bij naar boven gerichte warmtestroom (boven verwarmde ruimte) | 0,10 | 0,10 |
| Vloer boven buitenlucht | 0,17 | 0,04 |
| Vloer boven onverwarmde ruimte of kruipruimte | 0,17 | 0,17 |
| Vloer grenzend aan water / grond | 0,17 | 0,00 |
| Wand grenzend aan water / grond (kelderwand) | 0,13 | 0,00 |
| Wanden en overige constructies grenzend aan buitenlucht | 0,13 | 0,04 |
| Wanden en overige constructies niet grenzend aan buitenlucht | 0,13 | 0,13 |
Tabel 1: De waarden voor overgangsweerstand Rsi en Rse.
Warmteweerstand van een constructie opgebouwd
uit meerdere lagen (Rc waarde)
De warmteweerstand (Rc) van een vlakke
constructie bestaande uit meerdere lagen wordt volgens de Nederlandse Norm NEN
1068 berekend met:
Formule 3: 
Waarbij Σ Rm de som is van de afzonderlijke
materiaallagen in de constructie.
Rsi en Rse zijn de overgangsweerstanden zoals hierboven beschreven.
α Is een correctiefactor voor convectie (warmtetransport door luchtstroming) en uitvoeringsonnauwkeurigheden
in de constructie, in de meeste gevallen bedraagt deze correctiefactor: 0,05.
De eenheid van Rc is: m≤K/W
De Rc waarde wordt gemeten tussen het oppervlak
aan de ene zijde van de constructie, en het oppervlak aan de andere zijde.
De correctiefactor α voor de
berekening van de Rc waarde, heeft een
waarde overeenkomstig de volgende tabel:
| α | ||
| 1 | Indien een isolatielaag aan weerszijde een luchtlaag heeft van meer
dan 5 mm, tenzij er voorzieningen zijn getroffen om convectie tegen te gaan |
1,0 |
| 2 | Indien als isolatiemateriaal uitsluitend cellulair glas is toegepast | 0 |
| 3 | Indien het constructieonderdeel onder geconditioneerde en beheerste omstandigheden is vervaardigd (prefabricage met een attest met productcertificaat). |
0,02 |
| 4 | In alle overige gevallen | 0,05 |
Tabel 2: De correctiefactor α
Het onder punt 2 genoemde cellulaire glas, is het enige isolatiemateriaal dat volledig waterdicht, dampdicht, en luchtdicht is, dit is dus geheel iets anders dan glaswol.
Alternatieve berekening voor Rc waarde
Als alternatieve, en eenvoudiger rekenmethode wordt soms voor de Rc waarde
gebruikt:
Formule 4: Rc = Σ Rm
eenheid: m≤K/W
Hier komt dus geen correctiefactor aan te pas.
Als je alleen maar gebruik maakt van luchtdichte materialen, is deze formule
goed bruikbaar.
Als er isolatiematerialen in de constructie gebruikt worden, kun je beter
formule 3 gebruiken.
De totale warmteweerstand
De totale warmteweerstand (Rtotaal) is de warmteweerstand tussen de lucht aan de ene zijde, en
de lucht aan de andere zijde van
de constructie.
Om Rtotaal te berekenen, tellen we bij Rc de twee overgangsweerstanden Rsi en Rse op.
Dus:
Formule 5:
Rtotaal = Rse + Rc + Rsi
eenheid: m≤K/W
De U-waarde
De warmtedoorgangscoŽfficient U van een
constructie wordt berekend uit:
Formule 6: U = 1/ Rtotaal eenheid: W/m≤K
Voor sommige materialen zoals vensterglas wordt de U-waarde door de fabrikanten gespecificeerd (en niet de λ waarde).
Voorbeelden:
|
Soort glas |
U-waarde in W/m≤K |
| Enkel glas | 5,7 |
| Dubbel glas (4-6-4 mm) | 3,3 |
| Dubbel glas (4-12-4 mm) | 3,0 |
| HR dubbelglas | 1,8 W/m≤K |
| HR+ dubbelglas | 1,4 |
| HR++ dubbelglas | 1,1 |
| Triple glas | 0,5 |
Tabel 3: Voorbeelden van U-waarde bij glas.
De U-waarde werd voorheen ook wel k-waarde
genoemd.
Als je de U-waarde van een constructie al weet, kun je deze direct invullen in
de isolatie calculator, en gelijk verder gaan met het berekenen van het
energieverlies.
Warmtestroom door een constructie
Als we de U-waarde van een constructie weten, is de warmtestroom door de
constructie te berekenen met:
Formule 7: Qw = U . A. ΔT
Waarbij:
Qw = De warmtestroom door de constructie . eenheid: W
(Watt).
U = U-waarde van de constructie. eenheid: W/m≤K
A = Oppervlakte van de constructie. eenheid: m≤
ΔT = Verschil in luchttemperatuur tussen binnen en buiten (of tussen warme en koude
kant van constructie). eenheid: įC.
Deze berekening gaat alleen op als de
constructie geen direct zonlicht opvangt.
Als er direct zonlicht op bijvoorbeeld een buitenmuur valt, kan deze in enkele
uren tijd wel meer dan 20 įC warmer worden dan de buitenlucht, waardoor de warmtestroom
van binnen naar buiten
sterk afneemt.
Sterker nog, we kunnen dan een warmtestroom van buiten naar binnen krijgen,
terwijl de luchttemperatuur buiten toch lager is dan binnen.
Binnen oppervlakte temperatuur van de constructie
De binnenzijde van een constructie zal een oppervlakte temperatuur hebben welke
niet gelijk is aan de luchttemperatuur binnen.
Dit wordt veroorzaakt door de warmtestroom door de constructie, welke over de
overgangsweerstand Rsi een bepaalde temperatuurval (ΔT_Rsi) veroorzaakt.
Formule 8: ΔT_Rsi = ΔT . Rsi /
Rtotaal
Dit is hetzelfde als: ΔT_Rsi = ΔT . Rsi . U
Waarbij:
ΔT_Rsi = Het temperatuurverschil tussen de binnenlucht en het binnenoppervlak van de
constructie in įC.
ΔT = Verschil in luchttemperatuur tussen binnen en buiten (of tussen warme en koude
kant van constructie). eenheid: įC.
Rsi = Overgangsweerstand materiaal - lucht, aan de binnenzijde van de
constructie. eenheid: m≤K/W
Rtotaal = totale thermische weerstand van de constructie.
eenheid: m≤K/W
U = U-waarde van de constructie.
eenheid: W/m≤K
Energieverlies door een constructie
Als we de warmtestroom Qw vermenigvuldigen met een tijdsduur t (in seconden) krijgen
we de energie E (in Joule) welke in dat tijdsbestek door de constructie gaat.
Ofwel:
Formule 9: E = Qw . t
Waarbij:
E = Energie welke door de constructie gaat (het energieverlies), in J (Joule).
Qw = De warmtestroom door de constructie.
eenheid: W
t = Tijdsduur eenheid: seconden
Deze formule om de energie door de constructie te berekenen is alleen bruikbaar
als het temperatuurverschil over de constructie constant is.
Bij veel praktijkgevallen, waarbij de constructie in contact staat met de
buitenlucht, is het temperatuurverschil over de constructie echter niet
constant.
Energieverlies bij een constructie in contact met buitenlucht
Bij een constructie welke in contact staat met de buitenlucht, b.v. een muur of
dak van een huis, kunnen we het energieverlies berekenen door gebruik te maken
van
graaddagen.
Het energieverlies wordt dan:
Formule 10: E = U. A. G. 86400
Waarbij:
E = Energie welke gedurende die periode door de constructie gaat (het energieverlies), in J (Joule).
U = U-waarde van de constructie. eenheid: W/m≤K
A = Oppervlakte van de constructie. eenheid: m≤
G = Aantal graaddagen in die periode (niet de "gewogen graaddagen").
86400 = Aantal seconden per dag
Het aantal graaddagen bedraagt in midden Nederland ongeveer 2900 per jaar.
Voor het bepalen van het aantal graaddagen, ga naar de:
graaddagen
calculator.
Het berekenen van het energieverlies met behulp van graaddagen kan
afwijken van het werkelijke energieverlies, doordat:
- Er geen rekening wordt gehouden met zonnestraling op de
constructie.
- Er geen rekening wordt gehouden met wind op de
constructie.
- De binnentemperatuur niet constant hoeft te zijn
Zolang er geen direct zonlicht op de constructie kan vallen geeft deze methode
een goede indicatie van het energieverlies door de constructie.
Als er wel direct zonlicht op de constructie kan vallen, zal deze daardoor
opwarmen.
Hierdoor neemt het energieverlies van binnen naar buiten af.
Het gevolg is dat het energieverlies op jaarbasis vanwege de invloed van de zon,
(veel) lager is dan de berekende waarde uit formule 10.
De energie in Joule kunnen we omrekenen naar elektrisch verbruik (aantal
kWh), door te delen door 3.600.000.
Of naar gasverbruik (m≥ gas) door te delen
door 30.000.000 (dit is een globale waarde, hangt af van Cv-ketel rendement).
Warmtetransport in een luchtspouw
Voor het warmtetransport in een luchtspouw worden 3 mogelijke situaties onderscheiden, afhankelijk van
de hoeveelheid ventilatie openingen tussen de spouw en de buitenzijde (koude
zijde) van de constructie.
Ventilatie openingen kunnen bij een spouwmuur bijvoorbeeld bestaan uit open stootvoegen,
maar ook uit scheuren in het metselwerk.
Ook kan de bovenzijde van een spouwmuur (onder de dakpannen) volledig open zijn.
1- Een niet geventileerde spouw, hierbij zijn er tot maximaal 500 mm≤
ventilatie openingen per strekkende meter gevel naar de spouw.
Bij een spouwbreedte vanaf 18 mm zal de warmteweerstand van de spouw een
maximumwaarde bereiken van ongeveer 0,18 m≤K/W.
2- Een zwak geventileerde spouw, hierbij zijn er 500 - 1500 mm≤
ventilatie openingen per strekkende meter gevel.
Een zwak geventileerde spouw heeft een maximum warmteweerstand van ongeveer 0,09 m≤K/W.
3- Een sterk geventileerde spouw heeft meer dan 1500 mm≤
ventilatie openingen per strekkende meter gevel.
Bij een sterk geventileerde spouw is de warmteweerstand van de spouw 0,00 m≤K/W.
De isolerende werking van de lagen aan de buitenzijde van de spouw mag dan ook
niet meer worden meegerekend, de warmteweerstand van deze lagen moet op nul gesteld worden.
Een sterk geventileerde spouwmuur (zonder
isolatie in de spouw) zal dan ook net zo slecht isoleren als een enkel steens
muur.

Figuur 2:
De warmtedoorgangscoŽfficient (k waarde is hetzelfde als U waarde) van een niet
geventileerde verticale luchtspouw als functie van de spouwbreedte.
Uit bovenstaande grafiek blijkt dat de meeste warmte de spouw oversteekt via straling.
Alleen bij een zeer smalle spouw is de geleiding de belangrijkste factor in het
warmtetransport.
De k waarde van de luchtspouw (in figuur 2) is tussen 18 en 70 mm spouwbreedte min
of meer constant.
Daarmee is ook de warmteweerstand (Rm) van de luchtspouw bij deze breedtes
ongeveer constant, want Rm = 1/k.
| Niet geventileerde spouw | zwak geventileerde spouw | |
| Verticale luchtspouw (spouwmuur enz.) |
Rm = 0,18 m≤K/W | Rm = 0,09 m≤K/W |
| Horizontale luchtspouw bij opwaartse warmtestroom (vloer boven verwarmde ruimte) |
Rm = 0,14 m≤K/W | Rm = 0,07 m≤K/W |
| Horizontale luchtspouw bij neerwaartse warmtestroom. (vloer boven onverwarmde ruimte) |
Rm = 0,21 m≤K/W | Rm = 0,105 m≤K/W |
Tabel 4: Maximum warmteweerstand (Rm waarde) van een luchtspouw, bij verticale en horizontale plaatsing van de spouw.
Een sterk geventileerde spouw heeft steeds een warmteweerstand van: Rm = 0,00 m≤K/W.
Diverse bronnen geven aan, dat de Rm waarde bij een zeer brede spouw ( b.v. meer
dan 10 cm breed) weer zal afnemen, vanwege de toenemende invloed van convectie
in de spouw.
Maar exacte getallen of formules heb ik daar niet voor gevonden.
In de isolatie calculator blijft de Rm waarde bij toenemende spouwbreedte
constant op de waarde uit tabel 4.
Bij een luchtspouw in een schuin dak (tot 75 į)
gebruik ik de Rm waarde van een "horizontale luchtspouw bij opwaartse
warmtestroom".
Wellicht is dit niet helemaal goed, maar ik heb er niets beters voor gevonden.
De warmtegeleidingscoŽfficiŽnt λ van een
(zwak- of niet geventileerde) luchtspouw is niet constant, maar afhankelijk van de spouwbreedte.
Voor een zeer smalle spouw komt deze in de buurt van de λ waarde van lucht
(0,023 W/mK).
Bij een bredere spouw neemt de λ waarde toe.